ANSWER:
Part 1:
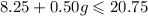
Part 2:

Part 3:
The answer is only reasonable to deduce the maximum number, the interval is not reasonable because it includes negative numbers, which is not possible. The answer is only reasonable if g goes from 0 to 25
Explanation:
Given:
Price per game: $0.5
Admission price: $8.25
If we have a total of $20.75, we establish the following inequality:
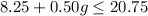
We solve for g:

We graph this:
In other words, that amount of money is limited to 25 games, so the answer makes sense, but if we see it from the graph, we can see that g can take negative values, which does not make sense.
Therefore, it is only reasonable to know the maximum limit, the answer as an interval does not make sense.