Question

A. If a particular ligament has an effective spring constant of 167 N/mm as it is stretched, what is the tension in this ligament when it is stretched by 0.720 cm?B. If a particular ligament has an effective spring constant of 167 N/mm as it is stretched, what is the elastic energy stored in the ligament when stretched by 0.720 cm?

Answer 1

Part (A)

The tension in the ligament is equal to the force acting on ligament. The expression for the tension in ligament is,

`F=kx`

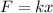
Substitute the given values,

`\begin{gathered} F=(167\text{ N/mm)(}\frac{1\text{ mm}}{10^(-3)\text{ m}})\text{(0.720 cm)(}\frac{1\text{ m}}{100\text{ cm}}) \\ =1202.4\text{ N} \end{gathered}`

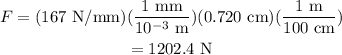
Thus, the tension in the ligament is 1202.4 N.

Part (B)

The elastic energy stored in the ligament can be given as,

`U=(1)/(2)kx^2`

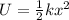
Substitute the known values,

`\begin{gathered} U=(1)/(2)(167N/mm)(\frac{1\text{ mm}}{10^(-3)\text{ m}})(0.720cm)^2(\frac{1\text{ m}}{100\text{ cm}})^2(\frac{1\text{ J}}{1\text{ Nm}}) \\ \approx4.33\text{ J} \end{gathered}`

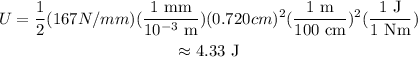
Thus, the elastic potential stored in the ligament is 4.33 J.