When rotating an image about a point not in the origin, we first subtract the coordinates of the point of the image to the cooridinates of the point of rotation.
We get,
Original point: (5, -10)
Point of rotation: (-3, 1)
New coordinate: [5 - (-3), -10 - (1)] = (8, -11)
At 180 Degree rotation,
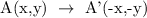
We get,
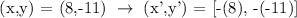
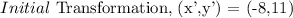
For the final transformation, let's add back the point of rotation to the transformed points:
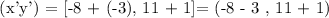
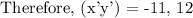
Therefore, the answer is 1 : (-11,12).