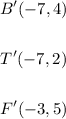We need to find the coordinates of the vertices of triangle B'T'F'. They correspond to a translation of the vertices of triangle BTF, with coordinates:
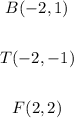
When we translate a point P(x,y) 5 units to the left and 3 units up, we obtain the point:
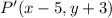
Therefore, the original vertices are transformed as:
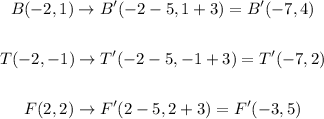
Therefore, the vertices of triangle B'T'F' are: