Given, the angle of depression for the observer's vision, α=5 degrees.
The height of the observer above sea level, h=300 feet.
Let x be the distance of the ship from the shore.
Using trigonometric property,

The ship is 3429 feet from the shore when the angle of depression for the observer's vision is 5 degrees.
After watching the ship for 46 seconds, the angle of depression for the observer's vision, α=12 degrees. Let x be the distance of the ship form the shore when the angle of depression for the observer's vision is 12 degrees. Using trigonometric property,
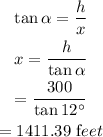
Therefore, the ship is 1411.39 feet from the shore when the angle of depression for the observer's vision is 12 degrees.
The distance travelled by the ship in t=46 s is
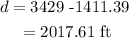
Hence, the speed of the ship is,
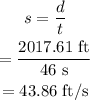
The speed of the ship is obtained as 43.86 ft/s.
When the observer initially spotted the ship, the distance from the shore to the ship is x=3429 ft.
The time taken by the ship to crash into the shore after the observer initially spotted the ship is,
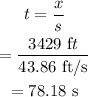
Therefore, the ship crash ito the shore after 78.18 s from the time the observer initially spotted the ship.