Question

Give an example of an odd degree polynomial but is NOT an odd function

Answer 1

Ok, so

We want to find an odd degree polynomial but is NOT an odd function.

This polynomial could be:

`x^3+2x^2-5x`

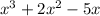
This is an odd degree polynomial because the highest degree is 3 which is an odd number.

Now, we're going to check that this isn't an odd function.

An odd function is supposed to satisfy that:

`f(-x)=-f(x)`

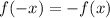
So, we're going to check this with our example:

`\begin{gathered} f(-x)=(-x)^3+2(-x)^2-5(-x) \\ f(-x)=-x^3+2x^2+5x \end{gathered}`

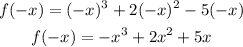
Now, let's make - f(x):

`-f(x)=-x^3-2x^2+5x`

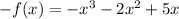
As you can see, these expressions aren't the same.

`f(-x)\\e-f(x)`

Therefore, the function is not odd.