Assuming the gas in question behaves as an ideal gas, we can use the Ideal Gas Law:
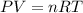
Where P is the pressure, V is the volume, n is the number of moles, R is the Ideal Gas Constant and T is the absolute temperature.
We have to match the units from R and the other variables.
The pressure is in kPa, so we can look for a R value that is also in kPa.
One such value is:

But the volume unit is in L, so we need to convert the volume we have:
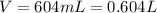
Now, we have:
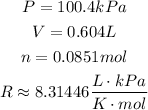
Solving the equation for T and substituting the values, we have:

So, the temperature is approximately 85.7 K.