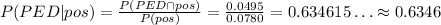Question

Plase help with this questions pls . And the parts of the question

Answer 1

Using the probability tree on the question, we can complete it with the probabilities.

In the first division, there are 5% of players that use PED, so we have 0.05 on the top branch and 0.95 on the bottom.

On the second branch of the top, we know that they are using, and the test when they are using gives 1% negative and 99% positive, so the branch PED - positive is 0.99 and the branch PED - negative is 0.01.

On the second branch of the bottom, we have the players who do not use PED, so we know that they have positive in 3% and negative in 97%, so doesn't use PED - positive is 0.03 and doesn't use PED - negative is 0.97.

So, we have:

We wil use this for a, b and c:

a) The probability for both uses PED and test positive is the product of the probability of he uses PED (PED) and the probability of positive given he uses PED (pos | PED):

`\begin{gathered} P(PED\cap pos)=P(PED)\cdot P(pos|PED) \\ P(PED\cap pos)=0.05\cdot0.99=0.0495 \end{gathered}`

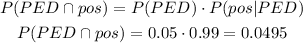
b) This probability is equal to both positives, the players who uses PED and the players who doesn't use PED.

It is the sum of the probability that a player uses PED and test positive (PED ∩ pos) and the probability of he doesn't use PED and test positive (NPED ∩ pos). So, we have:

`\begin{gathered} P(PED\cap pos)=0.0495 \\ P(NPED\cap pos)=P(NPED)\cdot P(pos|NPED) \\ P(NPED\cap pos)=0.95\cdot0.03=0.0285 \end{gathered}`
`\begin{gathered} P(pos)=P(PED\cap pos)+P(NPED\cap pos) \\ P(pos)=0.0495+0.0285 \\ P(pos)=0.0780 \end{gathered}`

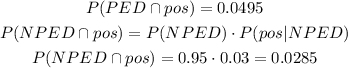
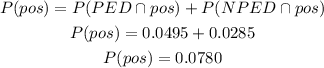
c) Given the player tests positive means the total we are working with is only the positive results, so the 0.0780. From these, we want the ones that uses PED, so the uses PED and positive (PED ∩ pos). The probability will be the players who uses PED and tests positive (PED ∩ pos) divided by all players that tests positive (pos):

`P(PED|pos)=(P(PED\cap pos))/(P(pos))=(0.0495)/(0.0780)=0.634615\ldots\approx0.6346`