Question

Kelsey deposited 800.00 in a savings account earning 14% interest, compounded annually. To the nearest cent, how much interest will she earn in 5 years?

Answer 1

The accrued amount of an investment is equal to the sum of the principal amount and the interest earned:

`A=P+I`

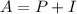
Write the expression in terms of the interest:

`I=A-P`

To calculate the interest, the first step is to determine the accrued amount after 5 years.

The savings account compounds annually, to determine the accrued amount you have to apply the following formula:

`A=P(1-(r)/(n))^(nt)`

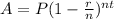
Where

A is the accrued amount

P is the principal amount

r is the interest rate expressed as a decimal value

t is the time in years

n is the number of compounding periods

The principal amount is P= $800

The interest rate of the account is 14%, to express it as a decimal value, divide it by 100

`\begin{gathered} r=(14)/(100) \\ r=0.14 \end{gathered}`

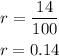
The time period for the investment is 5 years.

The account compounds annually, which means that there is only one compounding period per year, so, n=1.

Calculate the accrued amount:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=800(1+(0.14)/(1))^(1\cdot5) \\ A=800(1+0.14)^5 \\ A=800(1.14)^5 \\ A=1540.33 \end{gathered}`

After 5 years the accrued amount will be A= $1540.33

Finally, calculate the interest:

`\begin{gathered} I=A-P \\ I=1540.33-800 \\ I=740.33 \end{gathered}`

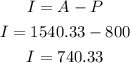
After 5 years she will have $740.33 of interest.