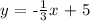Question

Write the equation of the line that is perpendicular to the graph of 3x-y=5, andwhose y-intercept is 5.

Answer 1

`y\text{ = -}(1)/(3)x\text{ + 5 or y = -0.33x + 5}`

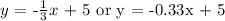
Step-by-step explanation

We have that the equation of the line is perpendicular to:

3x - y = 5

It is important to note that a linear equation is written generally as:

y = mx + c

where m = slope

c = y intercept

So, we need to find the slope of the new line.

A line that is perpendicular to another line has a negative inverse slope of that line.

Let us first identify the slope of the given line.

We have:

3x - y = 5

=> 3x - 5 = y

or

y = 3x - 5

So, we see that the slope is 3.

We now need to find the negative inverse of this value to find the slope of the line we need.

That is:

`\text{slope = }(-1)/(3)\text{ = -}(1)/(3)`

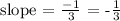
Therefore, the slope of the perpendicular line is -1/3.

We have that the y intercept is 5.

Therefore, the line perpendicular to 3x - y = 5 and with y intercept of 5 is:

`y\text{ = -}(1)/(3)x\text{ + 5}`