Question

The weights of bags of baby carrots are normally distributed, with a mean of 28 ounces anda standard deviation of 0.34 ounce. Bags in the upper 4.5% are too heavy and must berepackaged. What is the most a bag of baby carrots can weigh and not need to berepackaged?

Answer 1

In order to find the maximum weight, first we need to find the value of z that corresponds to the upper 4.5%.

To do so, let's find the value of z with a score of:

`score=100\%-4.5\%=1-0.045=0.955`

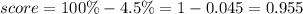
Looking at the z-table, the value of z for a score of 0.955 is equal to 1.695.

Now, to find the maximum weight x, we can use the formula below:

`z=(x-\mu)/(\sigma)`

Where μ is the mean and σ is the standard deviation.

So, using the given values, we have:

`\begin{gathered} 1.695=(x-28)/(0.34) \\ x-28=1.695\cdot0.34 \\ x-28=0.5763 \\ x=28.5763 \end{gathered}`

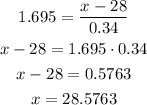
Rounding to two decimal places, we have a weight of 28.58 ounces.