Question

4. Identify the domain and range, draw a mapping, then state if the relation is a function.a) (4, 6) (6,-5) (4, 2) (6, 6)

Answer 1

We can start by looking at the points.

We can see that the relation is defined for x=4 and x=6.

`\begin{gathered} \text{Dom}\colon x\in\left\lbrace 4,6\right\rbrace \\ \end{gathered}`

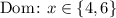
The image, that is the values that the dependant variable takes, are y=6, -5 and 2

For this relation to be a function, we have to have one and only one value for "y" for each value of "x" in the domain.

We can already see that for x=4, we have two values for y (y=6 and y=2), so we can conclude that this relation is not a function.

We can draw the points in an xy-plane and get: