x-5y = 4
-7x+35y = k
Isolating y in both equations,
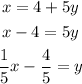
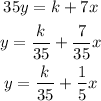
If both equations are equal, then there are infinitely many solutions. This criterion is satisfied if
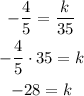
Since both equations have the same slope, if they don't have the same y-intercept then there will be no solution for the system of equations, that is,
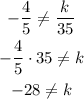
The given system has no solution for all real numbers k except k= -28
The given system has infinitely many solutions for k= -28