Question

A mass M=16kg is pulled along a horizontal floor, with a coefficient of kinetic friction MK=0.22, for a distance d=7m. Then the mass is continued to be pulled up a frictionless incline that makes an angle theta=39 degrees with the horizontal. The entire time the massless rope used to pull the block is pulled parallel to the incline at an angle theta=39 degrees (This the incline it is parallel to the surface) and has a tension T=50N.1) How far up the incline does the block travel before coming to rest?2) what is the work done by gravity as it comes to rest?

Answer 1

Part (1)

The free body daigram of the block on the inclined plane can be shown as,

According to work energy theorem,

`W=(1)/(2)mv^2-(1)/(2)mu^2`

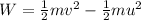
The work done on the block can be expressed as,

`W=Td-mg\sin \theta d`

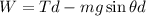
Plug in the known expression,

`\begin{gathered} Td-mg\sin \theta d=(1)/(2)m(0)^2-(1)/(2)mu^2 \\ d(T-mg\sin \theta)=-(mu^2)/(2) \\ d=-(mu^2)/(2(T-mg\sin \theta)) \end{gathered}`

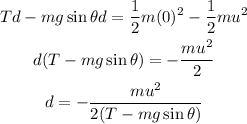
Substitute the known values,

`\begin{gathered} d=-\frac{(16kg)(5.293m/s)^2}{2((50N)(\frac{1kgm/s^2}{1\text{ N}})-(16kg)(9.8m/s^2)\sin 39} \\ =-(448.25kgm^2s^(-2))/(2(50kgm/s^2-98.7kgm/s^2)) \\ =-(448.25kgm^2s^(-2))/(2(-48.7kgm/s^2)) \\ \approx4.60\text{ m} \end{gathered}`

Thus, the distance travelled by the block is 4.60 m.

Part (2)

The work done by gravitational force is given as,

`W=-mg\sin \theta d`

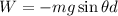
Substitute the known values,

`\begin{gathered} W=-(16kg)(9.8m/s^2)\sin 39(4.60\text{ m)(}\frac{1\text{ J}}{1kgm^2s^(-2)}) \\ =-(721.28\text{ J)(}0.629) \\ =-453.7\text{ J} \end{gathered}`

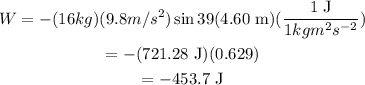
Thus, the work done by gravitational force is -453.7 J.