Solution:
Given:
where;

A right triangle can be extracted from the image above,
Applying the Pythagoras theorem to the right triangle,
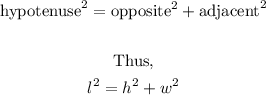
To find w, substitute the known values into the formula,
![\begin{gathered} l^2=h^2+w^2 \\ 20^2=16^2+w^2 \\ 400=256+w^2 \\ 400-256=w^2 \\ 144=w^2 \\ w=\sqrt[]{144} \\ w=\pm12 \\ Si\text{nce the problem is on the distance to hold the base of the ladder, we pick the positive value only.} \\ \text{Thus,} \\ w=12ft \end{gathered}]()
Therefore, the distance from the wall that the base of the ladder should be while they climb back in is 12 feet.
Hence, option D is the correct answer.