Question

19 Put le Together Use what you have learned to complete this task Graph each pair of functions on the same grid using x values of 0, 1, 2, 3, and 4 Function Pair A y X + 1 and y 2x+1 Function Pair B y x + 3 and y X+4 y TO y 10 6 5 4 2 2 Part A Answer these questions about Function Pair A. i Are the functions linear or nonlinear? ii Do the functions have the same or different rates of change and initial values? ili How can you describe graphs of other pairs of linear functions with the same similarities and differences in the rates of change and initial values? Part B Answer the questions in A.1, A.li, and A.l for Function Pair B.

Answer 1

Function Pair A consists of two linear functions with different rates of change and initial values. Other pairs of linear functions with the same similarities in rates of change and initial values will have parallel graphs.

Step-by-step explanation:

Function Pair A consists of two functions: y = x + 1 and y = 2x + 1.

i) Both functions in Pair A are linear functions because they can be written in the form y = mx + b, where m is the slope and b is the y-intercept.

ii) The functions have different rates of change and initial values. The rate of change for the first function is 1, and the rate of change for the second function is 2. The initial value for the first function is 1, and the initial value for the second function is also 1.

iii) Other pairs of linear functions with the same similarities in rates of change and initial values will have parallel graphs, while pairs with different rates of change will have non-parallel graphs.

Answer 2

Part A

For part A we have to graph the functions using the values 0, 1, 2, 3 and 4. to fin this values for each function we have to substitute the value of x in the function, the resulting value is y. For the function x+1 we have.

`\begin{gathered} x=0\rightarrow y=0+1=1 \\ x=1\rightarrow y=1+1=2 \\ x=2\rightarrow y=2+1=3 \\ x=3\rightarrow y=3+1=4 \\ x=4\rightarrow y=4+1=5 \end{gathered}`

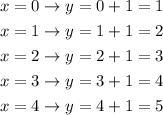
For the first function we have to plot the points

`(0,1),\text{ (1,2), (2,3), (3,4), (4,5)}`

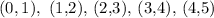
This points are shown in the following picture

For the function 2x+1, we have the

`\begin{gathered} x=0\rightarrow y=2(0)+1=1 \\ x=1\rightarrow y=2(1)+1=3 \\ x=2\rightarrow y=2(2)+1=5 \\ x=3\rightarrow y=2(3)+1=7 \\ x=4\rightarrow y=2(4)+1=9 \end{gathered}`

then we have to plot the points (0,1), (1,3), (2,5), (3,7) and (4,9). Doing this in the same grid we would have:

Now we join the point to see what type of functions we have, hence

Now we are prepared to answer the questions.

Are the functions linear or nonlinear?

The functions are linear.

Do the functions have the same or different rates of change and inicial values?

The functions have the same inicial value but they don't have the same rate of change. (From the graphs we notice that they start in the same point but the black one (2x+1) has a bigger rate of change. Two linear functions have the same rate of change if and only if they are parallel)

How can you describe graphs of other pairs of linear functions with the same similarities and differences in the rates of changes and initial values?

In this case we see that the functions have the same form, that is

`y=mx+b`

Since in this case the linear functions have the same initial value this means that the b should be equal for both pairs but since the rate of change is different, then the slope m has to be different. Therefore we can describe another pair of linear functions with the same similarities and differences like

`\begin{gathered} y=m_1x+b \\ \text{and} \\ y=m_2x+b \end{gathered}`

Part B

We have to apply the same steps for the part B of the problem, but in this case the functions are y=x+3 and y=x+4.

For y=x+3 we have

`\begin{gathered} x=0\rightarrow y=0+3=3 \\ x=1\rightarrow y=1+3=4 \\ x=2\rightarrow y=2+3=5 \\ x=3\rightarrow y=3+3=6 \\ x=4\rightarrow y=4+3=7 \end{gathered}`

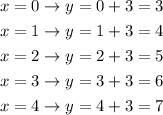
Then we have to plot the points (0,3), (1,4), (2,5), (3,6), (4,7). This points are shown in the following picture: