Answer: 1/2, 0, and -2
Given:
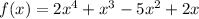
To know if a given value is a zero of a function, f(x) must be equal to 0. With this, we will substitute the given values and see which values will result in f(x)=0.
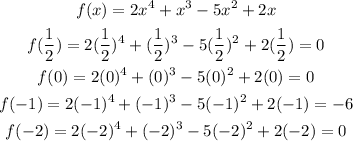
From these, we can see that the values 1/2, 0, and -2 resulted in f(x)=0. Therefore, the answers are 1/2, 0, and -2.