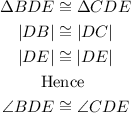Question

Given: ΔABE ≅ ΔACE and BD ≅ CD. Prove: ∠BDE ≅ ∠CDE

Answer 1

Given

`\begin{gathered} \\abla ABE \\ \text{And} \\ \\abla ACE \end{gathered}`

And

`\begin{gathered} |BD|\cong|CD| \\ \text{and } \\ |BE|\cong|CE| \\ \text{Correspounding sides of a congruent triangles are congruent} \end{gathered}`

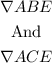
And looking at the common sides of the triangle

`\begin{gathered} |DE|\cong|DE|\text{ are common sides of the} \\ \\abla DBE\text{ and }\\abla DCE \\ |DE|\cong|DE|\text{ . Reflexive} \end{gathered}`

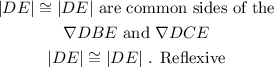
Using the sides Angle Sides theorem of congruency: If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.

`\begin{gathered} \Delta BDE\cong\Delta CDE \\ |DB|\cong|DC| \\ |DE|\cong|DE| \\ \text{Hence } \\ \angle BDE\cong\angle CDE \end{gathered}`