Given : the graph of the exponential function f(x)
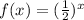
we need to graph the function :
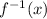
So, we need the inverse of the given function :
the inverse of the function will be the reflection of the graph over the line y = x
So, the graph will be as shown in the following image :
As shown the blue graph is the given graph f(x) = (1/2)^x
And the reflection over the line y = x will given the inverse of the function
Which is :
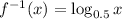
2. the domain of f^(-1) x is x > 0 = ( 0 , ∞ )
3. The range of f^(-1) x is : ( -∞ , ∞ )
4. Does f^(-1) x increase or decrease on its domain?
As x → ∞ , the function decrease
5. the equation of the vertical asymptote for f^(-1) x is : the y - axis
Which has the equation : x = 0