First, let's take a look at how the 2 teachers would be chosen.
Since ordering doesn't matter, we'll use the formula for a combination:
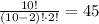
There are 45 different ways of choosing those 2 teachers out of the group of 10.
Now, let's take a look at how the 4 students would be chosen.
Since ordering doesn't matter here either, we'll use the formula for a combination:
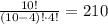
There are 210 different ways of choosing those 4 students out of the group of 10.
Now, for every possible combination of teachers chosen, there are 210 possible students groups. This way, in order to get the number of possible combinations for the comittee, we have to multiply 45 by 210:
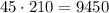
Therefore, there are 9450 different ways to form the comittee