According to the factor theorem, for any polynomial P(x), (x - a) is a factor if P(a) = 0.
The term (x - a) in this case is (x + 2), meaning that -a = 2, or a = -2.
Now, when evaluating P(-2), that is, replacing -2 anywhere we see an x, we should obtain 0 if (x + 2) is a factor of the polynomial given. Otherwise, it is not a factor.
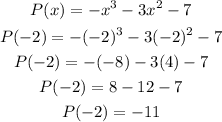
Then:
P(-2) = -11.
Having that P(a) is not 0, we can say that (x + 2) is not a factor of P(x)