Question

The function y=f(x) is graphed below. Plot a line segment connecting the points on ff where x=-7and x=-3Use the line segment to determine the average rate of change of the function f(x) on the interval −7≤x≤−3.

Answer 1

Step-by-step explanation:

Given;

We are given a cubic function as shown in the attached image.

Required;

We are required to determine the average rate of change of the function on the interval,

`-7\leq x\leq-3`

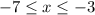
Step-by-step solution;

To solve this question using the line segment from the point where the value of the input is -7 up to -3, we would have the following;

Observe that the change in y is from 0 to -8 that is -8, while the change in x is from -7 to -3, that is 4.

In other words, what we have is;

`\begin{gathered} \Delta y=-8 \\ \Delta x=4 \end{gathered}`

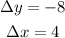
The average rate of change is given by the formula;

`ROC=(\Delta y)/(\Delta x)`
`ROC=(-8)/(4)`
`Rate\text{ }of\text{ }change=-2`

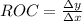
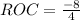
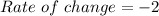
ANSWER:

The average rate of change on the given interval therefore is -2.