Question

A football is dropped from a height of 20 feet, and the ball bounces with each bounce 1/4 as high as the preceding one. What is the total height it would have traveled by the 8th bounce?

Answer 1

Given:

The height from whihc the ball is dropped, h=20 feet.

The height attained by the ball at each bounce can be written as a geometeric series.

Let a=20 feet be the first term of the series.

Since the ball bounces 1/4 as high as the preceding one, the common ratio of the sequence is,

`r=(1)/(4)`

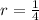
The sum of n terms in a geometric sequence is,

`S_n=(a(1-r^n))/(1-r)`

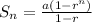
The total height traveled by the 8th bounce is given by the sum of 8 terms in a geometric series starting from a=20 ft.

The sum of the terms in a GP with a=20, r=1/4 and n=8 is,

`S_8=(20(1-((1)/(4))^8))/((1-(1)/(4)))=26.66`

Now, the total height traveled by the 8th bounce is,

`H=2* S_8-a=2*26.66-20=33.32\text{ ft}`

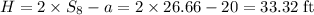
Hence, the total height the ball would have traveled by the 8th bounce is 33.32 ft.