Question

1. Write an exponential equation for each of the following table of values.Part a

Answer 1

The general form of an exponential function is the following

`\begin{gathered} y=ab^x \\ a\\e0 \\ b>1 \end{gathered}`

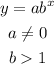
we can find the values for a and b using the known values for x and y. First, notice that when x = 0, y =51, then, if we put these values on the general form, we get:

`\begin{gathered} 51=ab⁰=a(1)=a \\ \Rightarrow a=51 \end{gathered}`

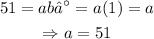
next, we have that when x = -1, y = 17. We also know now that a = 51, then, using this information, we can find the value of b:

`\begin{gathered} 17=51b^(-1) \\ \Rightarrow17=(51)/(b) \\ \Rightarrow17b=51 \\ \Rightarrow b=(51)/(17)=3 \\ b=3 \end{gathered}`

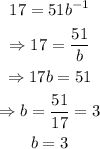
therefore, the exponential function is y = 51(3)^x