Compound Interest
Timber Inc. invested PV=$220,000 in a GIC at a rate of r=4.09% compounded monthly. We need to find the time it takes for the investment to have a value of FV=$306,000.
Recall PV is the present value of an investment, FV is its future value, r is the nominal interest rate, r = 0.0409 when expressed in decimal, and m = 12 because there are 12 compounding periods per year.
The periodic interest rate is calculated as:
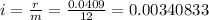
Here it's important to preserve as many decimals as possible because rounding can affect the ongoing calculations.
From the formula of the future value:
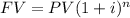
Where n is the number of compounding periods of the investment, we can solve for n as follows:
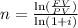
Substituting:
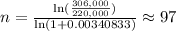
The investment should last for 97 months. Since one year has 12 months, 97 months represent 97/12 = 8 whole years. The remainder of this division is 1, so the time expressed in years+months is: 8 years and 1 month