ANSWER
the object will hit the ground at 4.793 seonds
Explanation
Given the function below
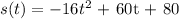
To find the value of t in seconds, let s(t) = 0
The new equation becomes
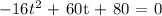
The quadratic function can be solved using the general quadratic formula
From the equation above,
Let a = -16, b = 60, and c = 80
![\begin{gathered} t\text{ = }\frac{-b\text{ }\pm\sqrt[]{b^2\text{ - 4ac}}}{2a} \\ t\text{ = }\frac{-(60)\pm\sqrt[]{60^2\text{ - 4 (-16)(80)}}}{2\text{ (-16)}} \\ t\text{ = }\frac{-60\pm\sqrt[]{3600\text{ + 5120}}}{-32} \\ t\text{ = }\frac{-60\text{ }\pm\sqrt[]{8720}}{-32} \\ t\text{ = }(-60\pm93.38)/(-32) \\ t\text{ = }\frac{-60\text{ + 93.38}}{-32}\text{ or }\frac{-60\text{ - 93.38}}{-32} \\ t\text{ = }(33.38)/(-32)\text{ or }(-153.8)/(-32) \\ t\text{ = -1.043 seconds or 4.793 secons} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c4bh43e4zdam54j648qk3x2jqpf8q3l6h0.png)
Hence, the object will hit the ground at 4.793 seonds