The vertices of traingle ABC are :
A (-2,-5),
B (-2,6)
C (9,-5)
Scale Factor : It is the ratio of the measurements of original size to the new size.
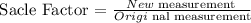
The coordinates of the new triangle A'B'C' is :
A'(-8, -20).
B'(-8, 24)
C' (36, -20).
Ratio of the coordinates are :
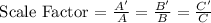
Substitute the value and simplify :

Scale Factor is 4.
Answer : Scale Factor is 4.