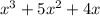Question

Write a polynomial equation with integer coefficients that has the given roots.

Answer 1

`x^(3)+5x^(2)+4x`

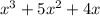
Explanation:

If we have the roots, which would be the zeros of an equation, then we convert each root into a factor and the product of all these factors is the polynomial, like this:

We multiply them like this:

`\begin{gathered} x\cdot \left(x+4\right)\left(x+1\right) \\ \\ x\cdot(x^2+x+4x+4) \\ \\ x^3+x^2+4x^2+4x \\ \\ x^3+5x^2+4x \end{gathered}`

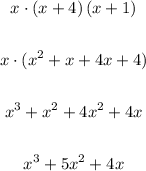
Therefore, the polynomial equation that has the given roots is:

`x^(3)+5x^(2)+4x`