We have to use the law of conservation of momentum, which states the following.

Using the definition of momentum (p = mv), we have the following.
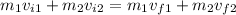
Using the given magnitudes, we replace them and we solve for the velocity of the lead car.
![\begin{gathered} 1,326\operatorname{kg}\cdot16((m)/(s))+1,206\operatorname{kg}\cdot13.3((m)/(s))=1,326\operatorname{kg}\cdot10.3((m)/(s))+1,206\operatorname{kg}\cdot v_(f2) \\ 21,216\operatorname{kg}\cdot(m)/(s)+16,039.8\operatorname{kg}\cdot(m)/(s)=13,657.8\operatorname{kg}\cdot(m)/(s)+1,206\operatorname{kg}\cdot v_(f2) \\ 21,216\operatorname{kg}\cdot(m)/(s)+16,039.8\operatorname{kg}\cdot(m)/(s)-13,657.8\operatorname{kg}\cdot(m)/(s)=1,206\operatorname{kg}\cdot v_(f2) \\ v_(f2)=\frac{23,598\operatorname{kg}\cdot(m)/(s)}{1,206\operatorname{kg}} \\ v_(f2)\approx19.57((m)/(s)) \end{gathered}]()
Therefore, the velocity of the lead car after the collision is 19.57 meters per second.