Question

The manufacturing engineers of a renowned pizza brand reduced the manufacturing cost of a pizza delivery box by optimising the shape of the box.To achieve this cost optimisation, the engineers reduced the volume of the box by 25% by flattening the curved side of the box (illustrated by the dashed line) to shape it like a proper prism, as shown in the below diagram.24 cm2836 cm(a) Find the value of 20.(b) (i) Find the area of the sector of the top surface of the old box design:(ii) Find the area of the top surface of the newly designed box.If the volume of the old box design was 3277 cm³, find the volume, V, of the newly designed box. rounding your answer correct to the nearest cubic centimetre:(ii) Hence, find the value of h.

Answer 1

Given: A pizza box's volume has been reduced by 25% by flattening the curved side of the box. The dimensions of the box are given.

Required: To determine the angle, the area of the sector of the top surface of the old box design, the area of the top surface of the newly designed box, and the volume, V, of the newly designed box. Also, determine the height of the box, h.

Explanation: The given box is-

If we draw a perpendicular as shown in the figure, the angle is bisected, and the side 24 cm is also bisected as the triangle on the top is an isosceles triangle. This can be easily proved by showing that the smaller triangles on the top face are congruent.

Next, we can use the trigonometric ratio sine to determine the angle as follows-

`\begin{gathered} sin\theta=(12)/(36) \\ \theta=sin^(-1)((1)/(3)) \\ \theta=19.47\degree \end{gathered}`

Thus,

`2\theta=38.94\degree`

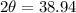
Next, the top of the new box is now a triangle with a base of 24 cm and a height-

`\begin{gathered} \text{ Height of triangle}=36cos\theta \\ =36cos(19.47\degree) \\ =33.94\text{ cm} \end{gathered}`

Hence, the area is-

`\begin{gathered} A=(1)/(2)*24*33.94 \\ =407.30\text{ cm}^2 \end{gathered}`

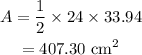
Now, the old box is a sector with a central angle of 38.94 degrees and a radius of 36 cm. Hence the area of the old box is-

`\begin{gathered} A=(\theta)/(360)*\pi r^2 \\ \end{gathered}`

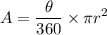
Substituting the values as-

`\begin{gathered} A=(38.94)/(360)*3.14*36*36 \\ =440.18\text{ cm}^2 \end{gathered}`

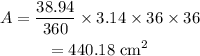
Lastly, the volume of the new box is 25% less than the old box. Hence the volume of the new box is-

`\begin{gathered} V=(25)/(100)*3277 \\ =819.25\text{ cm}^3 \end{gathered}`

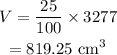
We can determine the height as follows-

`\begin{gathered} Vol=Area* h \\ \Rightarrow h=(Vol)/(Area) \end{gathered}`

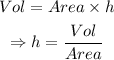
Hence,

`\begin{gathered} h=(819.25)/(407.30) \\ =2.011\text{ cm} \end{gathered}`

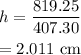
Final Answer: A)

`2\theta=38.94\degree`

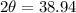
B) i) The area of the top of the old box=440.18 sq centimeters.

ii) The area of the top of the new box=407.30 sq centimeters.

C) i) The volume of the new box is 819 cubic centimeters.

ii) h=2.01 cm