Question

Suppose that $20,700 is invested in a certificate of deposit for 5 years at 10.5% annual interest to be compounded daily. How much interest will this investment earn?Round your answer to the nearest cent, if necessary. Note: 365 days in a year and 30 days in a month

Answer 1

Remember that the simple interest formula is:

`T=P(1+r)^n`

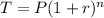
Where:

• T, is the total amount after the investment

,

• P, is the principal

,

• r, is the interest rate

,

• n, is the times the interest was compounded

To get the daily interest, we divide the annual interest rate by 365.

`\begin{gathered} r=(10.5)/(100)/365 \\ \\ \rightarrow r=(10.5)/(100\cdot365) \end{gathered}`

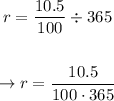
Since the interest compounds daily for 5 years,

`\begin{gathered} n=365\cdot5 \\ \rightarrow n=1825 \end{gathered}`

This way, we'll have that:

`\begin{gathered} T=20700(1+(10.5)/(100\cdot365))^(1825) \\ \\ \Rightarrow T=34989.86 \end{gathered}`

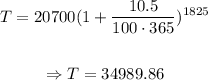
Substracting the principal from this amount, we can get the interest earned:

`34989.86-20700=14289.86`

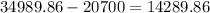
We can conclude that the interest earned was $14,289.86