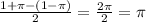Question

Find the amplitude, period, phase shift, and midline of this function.
`y = \sin( (\pi)/(6)x + \pi) - 3`

Answer 1

Standard form of a function is

`a\sin (bx+c)\pm d`
`y=\sin ((\pi)/(6)x+\pi)-3`

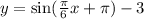
So by comparing the given equation to the standard form, we get

a=1, b=pi/6, c=pi, d=3

amplitude can be written as mod a or

`\lvert a\rvert=\lvert1\rvert=1`

So the amplitude is 1

Now for the period, we use generalization as

`(2\pi)/(\lvert b\rvert)\text{radians}`
`=(2\pi)/(\lvert(\pi)/(6)\rvert)=(2\pi)/((\pi)/(6))=2*6*(\pi)/(\pi)=12`

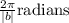
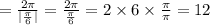
So the period is 12

Here, c is the phase shift, so c=pi

Hence phase shift is pi

Midline is the line that runs between maximum and minimum values

Since, the amplitude is 1 and the phase shift is -pi, the minimum and maximum values are

`\min =\text{ 1-}\pi\text{ }=1-\pi_{}`
`\max =1+\pi`

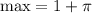
Midline will be the centre of region (1+pi, 1-pi)

So the midline will be

`(1+\pi-(1-\pi))/(2)=(2\pi)/(2)=\pi`