The given form to expand is (2x-4)^7
and we need to find the coefficient of x^3.
The binomial formula is
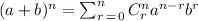
where n is a positive integer and a, b are real numbers, and 0 < r ≤ n
Substituting the values a = 2x, b = -4, n = 7 and r = 4
Then we have,
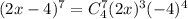
Now the coefficient of x^3 will be
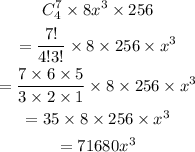
Hence, the coefficient will be 71680.