To solve this problem we can use the Triangle Inequality, which states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. If the sides of the triangle are:
• a = 5,
,
• b = 4,
,
• c = the missing side.
Mathematically we must have:
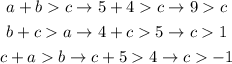
So the admissible values of the side c are given by the following inequality:
[tex]1From the answer options, the unique value that is not admissible is c = 1.
Answer
B. 1