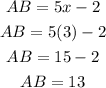Question

In the diagram shown below, points A, B, and, C are collinear. If AB=5x-2, BC=2x-3 and AC=9x-11, what is the length of AB? (diagram not drawn to scale)(1) 5(2) 6(3) 15(4) 28

Answer 1

By definition, Colinear points are those points (three or more) that lie on the same line.

Based on the the line shown in the picture, you can notice that:

`AB+BC=AC`

You know that:

`\begin{gathered} AB=5x-2 \\ BC=2x-3 \\ AC=9x-11 \end{gathered}`

So you can substitute them into the first equation:

`(5x-2)+(2x-3)=9x-11`

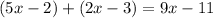
Having this equation, you can solve for "x":

`\begin{gathered} 5x-2+2x-3=9x-11 \\ 7x-2=9x-11 \\ -5+11=9x-7x \\ 6=2x \\ x=(6)/(2) \\ x=3 \end{gathered}`

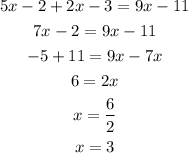
Knowing the value of "x", substitute it into the equation of AB and then evaluate, in order to find its length.

So, the length fo AB is:

`\begin{gathered} AB=5x-2 \\ AB=5(3)-2 \\ AB=15-2 \\ AB=13 \end{gathered}`