The probability of finding a five in the first draw, is the amount of '5' inside the deck(4) divided by the total amount of cards in the deck(52).
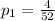
The probability of drawing a jack follows the same logic, but since this is the second draw and the cards are not replaced, the total amount of cards decreases by one. We have 4 jacks and 51 cards.
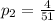
Since each draw is an independent event, the probability of both things happening at the same time is given by the product of the probabilities of each individual draw.
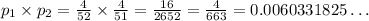
The probability of drawing a five and then drawing a jack is around 0.6%.