Question

A potter’s wheel moves from rest to an angular speed of 0.10 rev/s in 27.7 s.Assuming constant angular acceleration,what is its angular acceleration in rad/s2?Answer in units of rad/s2.

Answer 1

Answer:

The angular acceleration of the potter's wheel = 0.023 rad/s²

Step-by-step explanation:

At rest, the angular speed, w₀ = 0 rad/s

Final angular speed, w = 0.10 rev/s

Convert 0.10 rev/s to rad/s

`\begin{gathered} w=0.10*2\pi\text{ rad/s} \\ w=0.10*2*3.142 \\ w=0.6284\text{ rad/s} \end{gathered}`

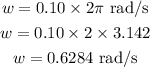
Time, t = 27.7 s

To find the angular acceleration, use the equation:

`w=w_0+\alpha t`

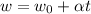
Substitute w = 0.6284 rad/s, w₀ = 0 rad/s, and t = 27.7 s into the equation above

`\begin{gathered} w=w_0+\alpha t \\ 0.6284=0+\alpha(27.7) \\ 27.7\alpha=0.6284 \\ \alpha=(0.6284)/(27.7) \\ \alpha=0.023rad/s^2 \end{gathered}`

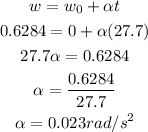
The angular acceleration of the potter's wheel = 0.023 rad/s²