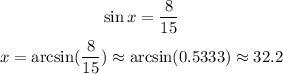arc functions are the inverse functions of the trigonometric function. So, if we have an angle, for instance, 60°, we can input it to a sin, cos or tan function to get the results:
![\begin{gathered} \sin 60\degree=\frac{\sqrt[]{3}}{2} \\ \cos 60\degree=(1)/(2) \\ \tan 60\degree=\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6h95h22selcv4hpb5w3skb6yz2apxknxrt.png)
The arc functions, arcsin, arccos and arctan, is the other way around: we have a sin/cos/tan value and want the corresponding angle, so:
![\begin{gathered} \arcsin (\frac{\sqrt[]{3}}{2})=60\degree \\ \arccos ((1)/(2))=60\degree \\ \arctan (\sqrt[]{3})=60\degree \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vkuzwavmeijlozibo9ko678blyu2ex8uz9.png)
9) To find the missing angles, e can use arc functions, the inverse functions of the trigonometric functions.
We have the opposite leg of the angle and the hypotenuse, so we have:
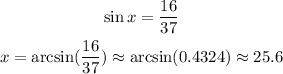
10) We want the adjacent leg, given the angle and the opposite leg, so we use tangent:
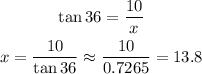
11) Just like 9, we want an angle given its opposite leg and hypotenuse. So we use sine: