Question

Solve the following system of equations using Gaussian or Gauss-Jordan elimination.

Answer 1

Okay, here we have this:

Considering the provided system of equation, we are going to solve it using Gauss-Jordan elimination, so we obtain the following:

So first let's reduce the matrix to echelon form, we have:

`\begin{gathered} \begin{bmatrix}{5} & {6} & -{4} \\ {2} & -{4} & {3} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix} \\ \end{gathered}`

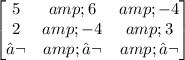
We perform the operation R2=R2-(2/5)R1:

`\begin{bmatrix}{5} & {6} & -{4} \\ {0} & {-(32)/(5)} & {(23)/(5)} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

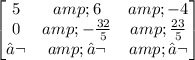
Now we apply the operation: R2=-(5/32)R2

`\begin{bmatrix}{5} & {6} & {-4} \\ {0} & {1} & {-(23)/(32)} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

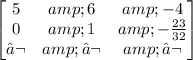
Now we apply the operation: R1=R1-6R2

`\begin{bmatrix}{5} & {0} & {(5)/(6)} \\ {0} & {1} & {-(23)/(32)} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

And finally we apply the operation: R1=1/5R1

`\begin{bmatrix}{1} & {0} & {(1)/(16)} \\ {0} & {1} & {-(23)/(32)} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

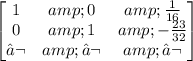
Finally we obtain that there is only one solution, the solution is: (1/16, -23/32).