The vertex for a quadratic equation of the form

is given by

In our case, b = -4 and a = -1; therefore,
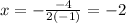

this is the x-coordinate of the vertex, the y-coordinate is
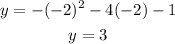
Hence, the coordinates of the vertex are
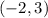
And since we have a negative sign on x^2, the parabola is concave down; therefore, the vertex is the maximum value.
The correct choice, therefore, is (-2, 3) maximum value