Question

Given θ is in the third quadrant, φ is in the second quadrant, sinθ=-5/13, and tanφ=-8/15. Find the value of sin(θ+φ)1) -171/2212) -21/2213) 171/221

Answer 1

We know that in a circle on the plane center at the origin the trigonometric functions are defined as:

`\begin{gathered} \sin \theta=(y)/(r) \\ \cos \theta=(x)/(r) \\ \tan \theta=(y)/(x) \end{gathered}`

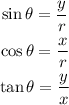
where x and y are the coordinates of the point (x,y) on the circle defined by the angle theta and r is the radius of the circle.

From this definition and the fact that:

`\tan \varphi=-(8)/(15)`

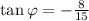
we have that, for angle phi:

`\begin{gathered} \lvert x\rvert=15 \\ \lvert y\rvert=8 \end{gathered}`

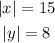
but we need to determine the correct sign for each component; to do this we have to remember that phi is in the second quadrant; in this quadrant the x coordinates are negative and the y coordinates are positive, this means that:

`\begin{gathered} x=-15 \\ y=8 \end{gathered}`

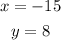
Now, to find the radius we remember that the circle defining the functions is centered at the origin, this means that the radius is the distance from the origin to the point with coordinates (-15,8), then we have:

`\begin{gathered} r=\sqrt[]{(-15)^2+(8)^2} \\ r=\sqrt[]{289} \\ r=17 \end{gathered}`

Now that we know the coordinates of the point defined by the tangent of phi we plug the values in the definitions of the trigonometric functions, then we have:

`\begin{gathered} \sin \varphi=(8)/(17) \\ \cos \varphi=-(15)/(17) \end{gathered}`

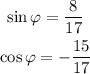
Now let's bring our attention to the theta angle. We know that the pythagorean identity states that:

`\sin ^2\theta+\cos ^2\theta=1`

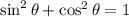
Plugging the value given for the sine of theta and solving for the cosine we have:

`\begin{gathered} (-(5)/(13))^2+\cos ^2\theta=1 \\ \cos ^2\theta=1-(-(5)/(13))^2 \\ \cos ^2\theta=(144)/(169) \\ \cos \theta=\pm\sqrt[]{(144)/(169)} \\ \cos \theta=\pm(12)/(13) \end{gathered}`

to determine the correct sign for the cosine we need to remember that the angle lies in the thirs quadrant, in this quadrant the sine is negative and the cosine is negative as well, then we conclude that:

`\cos \theta=-(12)/(13)`

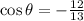
Let's sum up what we have so far:

`\begin{gathered} \sin \theta=-(5)/(13) \\ \cos \theta=-(12)/(13) \\ \sin \varphi=(8)/(17) \\ \cos \varphi=-(15)/(17) \end{gathered}`

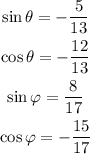
Now that we know the value for this functions we can calculate the sine function if we remember that:

`\sin (\theta+\varphi)=\sin \theta\cos \varphi+\sin \varphi\cos \theta`

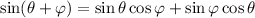
Plugging the values we know:

`\begin{gathered} \sin (\theta+\varphi)=(-(5)/(13))(-(15)/(17))+((8)/(17))(-(12)/(13)) \\ \sin (\theta+\varphi)=(75)/(221)-(96)/(221) \\ \sin (\theta+\varphi)=-(21)/(221) \end{gathered}`

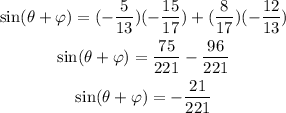
Therefore:

`\sin (\theta+\varphi)=-(21)/(221)`

and the correct answer is option 2