Given data:
* The mass of the first spherical object is,
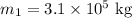
* The mass of the second spherical object is,
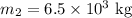
* The force of attraction between the objects is,
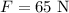
Solution:
The gravitational force of attraction between the spherical object in terms of the distance between their centers is,
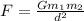
where G is the gravitational constant and d is the distance between the centers of spherical objects,
Substituting the known values,
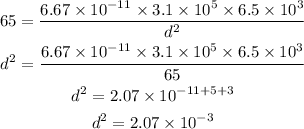
Thus, the distance between the centers is,
![\begin{gathered} d=\sqrt[]{2.07*10^(-3)} \\ d=\sqrt[]{0.207*10^(-2)} \\ d=0.455*10^(-1) \\ d=0.0455\text{ m} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/hfpvktksyojkx4nusdmwvyywz37zc607vh.png)
Hence, the distance between the centers is 0.0455 meters or 4.6 centimeters.