According to the Transformation rules for functions:
1) When a function f(x) is shifted left "k" units:
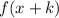
2) When it is shifted right "k" units:

3) When it is shifted up "k" units:
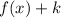
4) When it is shifted down "k" units:
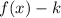
Observe in the graph attached that the vertex of the following parent function is located at the origin:
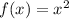
Knowing that the function g(x) is:
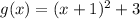
You can determine that the function g(x) is the function f(x) but shifted left 1 unit and shifted up 3 units.