Let x be the number of minutes and y be the total cost. Then, for plan A we have
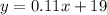
and for plan B, we have

In order to find the number of minutes where the plans cost the same, we need to find the intersection point of the two equations. Then, we need to solve the following system of equations:

Then, by substituting equation 2 into 1, we get
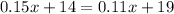
By subtracting 0.11x and 14 to both sides, we have
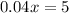
Then, x is given by
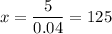
For what amount of calling do the plans cost the same? For one minute of calls, the plans cost the same at 125 calls.
Now, in order to find the cost, we need to substitute the last result into one of our 2 equations. If we substitute x=125 into equation 1, we have
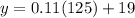
which gives
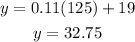
What is the cost when the two plans cost the same? The answer is $32.75