Question

What is the area of the parallelogram shown in the diagram?(3,3)(7,3)(2,1)(6,1)OA. 12 sq unitsB. Not enough information is given.OC. 8 sq unitsOD. 18 sq unitsOE. 42 sq units

Answer 1

Given the vertices of the parallelogram:

(3, 3), (7, 3), (2, 1), (6, 1)

Let's find the area of the parallelogram.

We have the parallelogram below:

To find the area of the parallelogram, apply the formula:

Area = base x height.

Let's find the length using the distance formula:

`b=√((y_2-y_1)^2+(x_2-x_1)^2)^`

Where:

(x1, y1) ==> (3, 3)

(x2, y2) ==> (7, 3)

Thus, we have:

`\begin{gathered} b=√((3-3)^2+(7-3)^2) \\ \\ b=√(0^2+4^2) \\ \\ b=4 \end{gathered}`

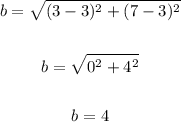
The length of the parallelogram is 4 units.

Also, let's find the width using the distance formula:

(x1, y1) ==> (3, 3)

(x2, y2) ==> (2, 1)

`\begin{gathered} W=√((1-3)^2+(2-3)^2) \\ \\ W=√((-2)^2+(-1)^2) \\ \\ W=√(4+1) \\ \\ W=√(5) \end{gathered}`

The width of the parallelogram is √5 units.

Distance from x to y = 1 unit.

To find the height, apply Pythagorean theorem:

`\begin{gathered} h=\sqrt{(√(5))^2-1^2} \\ \\ h=√(5-1) \\ \\ h=√(4) \\ h=2 \\ \end{gathered}`

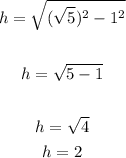
The height of the parallelogram is 2 units.

To find the area, we have:

Area = base x height

Area = 4 x 2

Area = 8 square units.

Therefore, the area of the parallelogram is 8 square units.

ANSWER:

C. 8 sq. units.