Question

A cannonball is launch straight upward at a speed of 15.0 meters per second from an initial height of 10.0 meters. determine the time that it takes for the cannonball to reach the ground

Answer 1

3.62 s

Step-by-step explanation

Given:

• The initial upward velocity of the cannonball, u = 15.0 m/s

,

• The initial height of the cannonball, y₀ = 10.0 m

Find:

• The time it takes for the cannonball to reach the ground, t

What we have to find is the time it will take for the cannonball to reach a height of y = 0. First, the cannonball travels upward until it reaches its maximum height. At this point, the ball stops and starts speeding up downwards, so, first, we can find the time it takes for the cannonball to reach its maximum height,

`v=u-gt\Rightarrow0=u-gt_(h,max)`

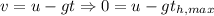
Solving for the time,

`t_(h,max)=(u)/(g)=(15.0m\/s)/(9.8m\/s^2)\approx1.53s`

Now, knowing that time, we can find what is the ball's maximum height,

`y_(max)=y_o+ut-(1)/(2)gt^2=10m+15m\/s\cdot1.53s-(1)/(2)\cdot9.8m\/s^2\cdot1.53^2s^2\approx21.48m`

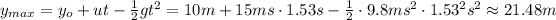
Now we have to find how long will it take for the cannonball to reach the ground when the initial velocity is 0 - since it is at its maximum height, and travel 21.48 m in total to the ground,

`y_(max)=(1)/(2)gt^2\Rightarrow t=\sqrt{(2y_(max))/(g)}=\sqrt{(2\cdot21.48m)/(9.8m\/s^2)}\approx2.09s`

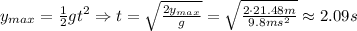
So, in total the cannonball traveled up for 1.53 seconds until its maximum height and, then, it traveled back down for 2.09 seconds until it reached the ground,

`t_(total)=1.53s+2.09s=3.62s`

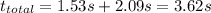
Hence, it takes 3.62 seconds for the cannonball to reach the ground.