The formula for the expected number of complaints is as follows:

Substitute the given values into the equation.
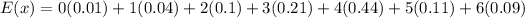
Simplify the right side of the equation. Multiply and then find the sum of the products.
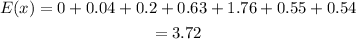
Thus, there are approximately 3.72 or 4 complaints in a day.