To solve this problem we have to state a system of equations and solve it.
Let x and y be the rates charged per hour by each mechanic.
The sum of x and y is 220:

The sum of 20x and 15y is 3875:
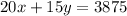
Solve the system by substitution:

Use the value of y to find x:
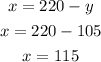
It means that the rates charged per hour by each mechanic were $115 and $105.