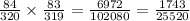Step 1
Write an expression for the probability of an event
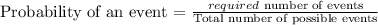
Required number of events = 84
Total number of events = 320
Step 2
Find the probability that both customers selected without replacement say service is poor.
![Pr(customersselectedsayserviceispoor\text{ ) + pr(}customersselectedwithoutreplacementsayserviceispoor\text{)}]()
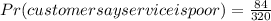
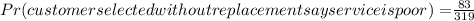
The final answer will be given as