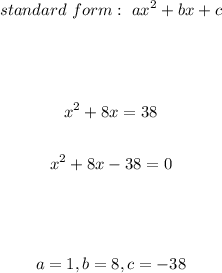In order to complete the square, let's analyze the coefficient of the variable x.
The coefficient is 8. Now, to complete the square, we need the square of half this value, that is:
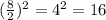
Now, to complete the square, let's add and remove 16 on the left side of the equation:
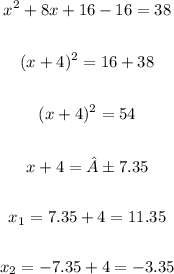
Now, let's find the coefficients a, b and c from the standard form: